球磨机——经验球径公式的局限性与误差

一经验球径公式是在大量试验资料或生产资料的基础上总结出来的数学模型。此种方法对于影响因素错综复杂而在理论上难于取得进展的球磨过程来说，仍不失为一种有用的方法。此类方法得出的公式其可贵之处在于它来源于实践而高于实践，既有可靠性也有实用性。在这以前的漫长岁月中，选矿工作者也正是利用这些经验球径公式加上自己的经验来解决磨机的球径，解决问题的。

但是，从球径经验公式产生的方法上不难看出它有自身的局限性，而且有较大的误差。尽管试验资料或生产资料是丰富的，但也仍然是有限的，或者是试验和生产的设备规格以及形式有限，或者是试验和生产的矿石种类有限，也或者是试验次数和生产时间有限，总之，资料的来源是有限的。这样，在有限的资料上总结出来的模型其使用范围也必然是有限的，跨越这个有限的范围也就失去可靠性。因此，经验公式一旦跨出总结它时所依据的资料范围，就必然产生大的误差。

即使对同样的试验和生产资料，不同的研究者采用的数学处理方法有别，因而得出的数学模型不相同，计算出的球径结果也不相同。另外，球径经验公式中均带有经验修正系数，不同的研究者根据各自的经验，所取的经验系数值不相同，自然算出的球径结果也不相同。

上述分析表明，研究者在什么条件下总结出来的经验球径公式适用于总结它时所限定的条件，如若把它推广应用，与限定的条件不同时必然产生较大误差，还必须再对它进行经验修正。认识经验公式的局限性是必要的，而针对局限性进行经验修正也是必要的，否则将产生较大的误差。

下面以我国选矿界常用的K.A拉苏莫夫经验球径公式的应用来说明经验公式的局限性与误差问题。

K.A拉苏莫夫根据某些平均条件提出，磨矿所需的钢球直径D_b与给矿粒度d的n次方成比例，若比例系数为i，则得：

D_b=idⁿ (5-14)

显然，不同的磨矿条件有不同的i及n值，对每个具体的磨矿条件都必须用实验方法求出i及n值，然后才能运用公式（5-14），这就是此公式的局限性。公式（5-14）的求解，必须对具有两个方程式的方程组求解，两个方程式才能求解两个未知数。假设给矿粒度d₁通过试验求出需要的球径是D_b1，则得一个方程式：

D_b1=idⁿ¹ (5-15)

再设给矿粒度d₂通过试验求出需要的球径是D_b2，则又得另一个方程式：

联立方程式（5-15）和（5-16），并求解此方程组的i和n:

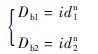
将式（5-17）代入式（5-16）得：

式（5-18）变换得：

式（5-19）两边取对数得：

即得：

式中(5-20)中，d₁，d₂，D_b1和D_b2均是已知数，故n可以求出。n值求出后返回代入式(5-17)，则i也可求出。

求出i及n后，就得出该特定条件下的球径D与给矿粒度d之间的通式：

D_b=idⁿ

也就可以由此通式计算该特定条件下各给矿粒度所需的球径。如果磨矿条件改变，必须采用同样的方法找出新的通式。这是此公式的局限性，不能跨越求解方程时的特定条件去使用。

此公式的问题在于，以粒度d₁和d₂进行试验，则得到的公式通式在d₁-d₂范围内应用时较为准确，若超过d₁-d₂范围应用时必然产生较大误差，因为岩矿的力学强度是随粒度变细而加大的。例如d₁和d₂的试验通常在实验室内进行，所用的给矿粒度通常在5mm以下，粒度较细，矿粒力学强度较高。而试验得出的通式，其参数是在d₁和d₂范围内求出的，如果推广用于d=10-25mm范围，求出的球径必然是偏大的，因为10-25mm矿块的力学强度比5mm及以下明显地小，则计算粗块下所需的球径必然偏大。例如，有人用5和3mm粒级在实验室做试验，求出i和n后得通式，再用通式计算25mm矿块所需的球径是125mm自己修正后的球径半理论公式计算，只需100mm就足够了。通过一年的工业试验，证明采用就足够了。通过一年的工业试验，证明采用100mm钢球比125mm钢球好得多。说明原来计算的球径是偏大的。这就是拉苏莫夫球径公式产生误差的原因所在。

由于K.A拉苏莫夫公式D_b=idⁿ需要做试验确定参数i和n，使用较麻烦。他又提出，对中硬矿石可以直接使用简便计算公式：

f=8-16范围的均算中硬矿石，f=16的矿石的强度为f=8的矿石的两倍，但计算用的同一公式，哪会有不产生较大误差的道理？而且，该简化公式广泛用于中硬矿石不同磨矿条件，产生的误差必然比公式（5-14）的更大。